MAKE A MEME
View Large Image
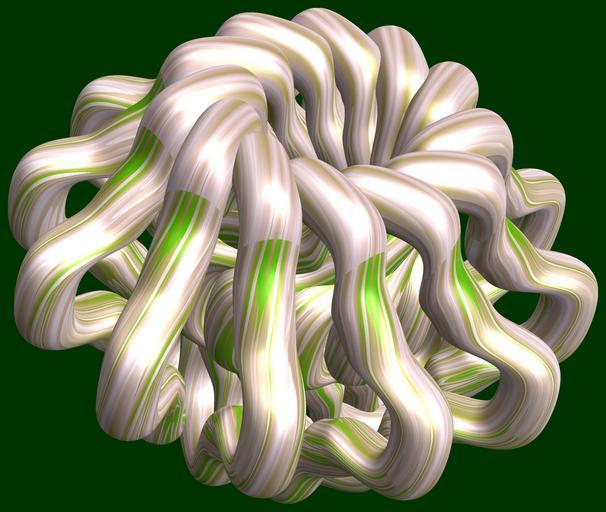
| View Original: | 12_crossing_tetra-tori_/_交差する十二個の四芒星環.jpg (3080x2602) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | www.flickr.com | More Like This | ||
| Keywords: mathematica 3d cg parametricplot3d texture torus 輪環 りんかん ドーナツ どーなつ 四芒星 しぼうせい 四光星 しこうせい 四稜星 しりょうせい プログラム コード code program algorithm コード アルゴリズム geometric sculpture geometricsculpture shape geometry sculpture mapping テクスチャ マッピング 模様 もよう design pattern デザイン パターン graphic グラフィック グラフィクス structure 意匠 構造 symmetry 対称性 たいしょうせい シンメトリー 対称 たいしょう algorithm SetOptions[ParametricPlot3D, PlotRange -> Full, Mesh -> None, Boxed -> False, Axes -> None, PlotPoints -> 300, ImageSize -> 3000, Background -> Darker[Green, 0.8], PlotStyle -> Directive[Specularity[White, 30], Texture[Import["D:/tmp/862.jpg"]]], TextureCoordinateFunction -> ({#4 + #5, #5/Pi} &), Lighting -> "Neutral"]; a = 5; (* center hole size of a torus *) b = 4; (* tetra-torus *) c = 3; (* distance from the center of rotation *) d = 12;(* number of torus *) f[v_] := Sin[2 Sin[Sin[Sin[v]]]]; x = (a - Cos[t] - f[b s]) Cos[s + Pi/(2 b)] + c; y = Sin[t] + c; z = (a - Cos[t] - f[b s]) Sin[s + Pi/(2 b)] + c; rot = Table[{x, y, z}.RotationMatrix[2 i Pi/d, {1, 0, 0}], {i, d}]; ParametricPlot3D[rot, {t, 0, 2 Pi}, {s, 0, 2 Pi}] (* --- The Texture *) SetOptions[ParametricPlot3D, PlotRange -> Full, Mesh -> None, Boxed -> False, Axes -> None, PlotPoints -> 300, ImageSize -> 3000, Background -> Darker[Green, 0.8], PlotStyle -> Directive[Specularity[White, 30], Texture[Import["D:/tmp/862.jpg"]]], TextureCoordinateFunction -> ({#4 + #5, #5/Pi} &), Lighting -> "Neutral"]; a = 5; (* center hole size of a torus *) b = 4; (* tetra-torus *) c = 3; (* distance from the center of rotation *) d = 12;(* number of torus *) f[v_] := Sin[2 Sin[Sin[Sin[v]]]]; x = (a - Cos[t] - f[b s]) Cos[s + Pi/(2 b)] + c; y = Sin[t] + c; z = (a - Cos[t] - f[b s]) Sin[s + Pi/(2 b)] + c; rot = Table[{x, y, z}.RotationMatrix[2 i Pi/d, {1, 0, 0}], {i, d}]; ParametricPlot3D[rot, {t, 0, 2 Pi}, {s, 0, 2 Pi}] (* --- The Texture *) | ||||