MAKE A MEME
View Large Image
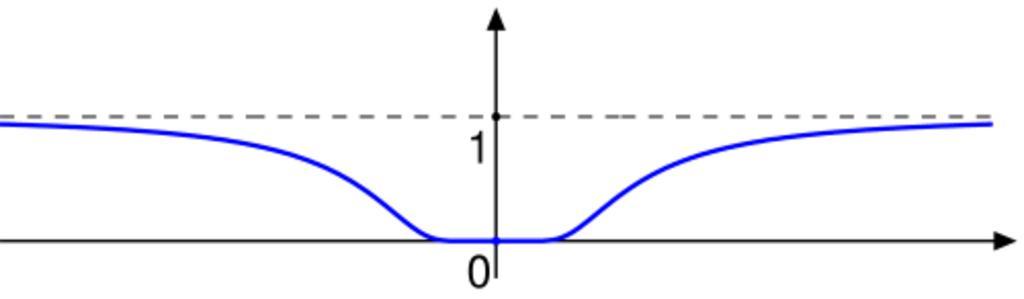
| View Original: | An infinitely differentiable function which is not analytic illustration.png (500x146) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: An infinitely differentiable function which is not analytic illustration.png en wikipedia Maksim page en wikipedia Source code Matlab <pre> <nowiki> function main thickness1 2; thickness2 1 5; arrowsize 10; arrow_type 2; ball_rad 0 03; blue 0 0 1; black 0 0 0; fontsize floor 20 ; dist 0 01; a -4; b 4; h 0 01; X a h b; Y zeros length X 1 ; for i 1 length X x X i ; if x 0 Y i 0; else Y i exp -1/x 2 ; end end figure 1 ; clf; hold on; axis equal; axis off arrow a 0 b+0 2 0 thickness2 arrowsize pi/8 arrow_type 0 0 0 arrow 0 -0 3 0 2 max Y thickness2 arrowsize pi/8 arrow_type 0 0 0 plot X Y 'linewidth' thickness1 'color' blue ; plot X 0 Y+1 'linewidth' thickness2/1 5 'color' black 'linestyle' '--' ; arrow b+0 1 0 b+0 2 0 thickness2 arrowsize pi/8 arrow_type 0 0 0 ball 0 0 ball_rad blue ; place_text_smartly 0 fontsize 5 dist '0' ; ball 0 1 ball_rad black ; place_text_smartly sqrt -1 fontsize 5 dist '1' ; saveas gcf 'An_infinitely_differentiable_function_which_is_not_analytic_illustration eps' 'psc2' function place_text_smartly z fs pos d tx p cos pi/4 +sqrt -1 sin pi/4 ; z z + p pos d fs; shiftx 0 0003; shifty 0 002; x real z ; y imag z ; H text x+shiftx fs y+shifty fs tx ; set H 'fontsize' fs 'HorizontalAlignment' 'c' 'VerticalAlignment' 'c' function ball x y r color Theta 0 0 1 2 pi; X r cos Theta +x; Y r sin Theta +y; H fill X Y color ; set H 'EdgeColor' color ; function arrow start stop thickness arrowsize sharpness arrow_type color draw a line with an arrow at the end start is the x y point where the line starts stop is the x y point where the line stops thickness is an optional parameter giving the thickness of the lines arrowsize is an optional argument that will give the size of the arrow It is assumed that the axis limits are already set 0 < sharpness < pi/4 determines how sharp to make the arrow arrow_type draws the arrow in different styles Values are 0 1 2 3 8/4/93 Jeffery Faneuff Copyright c 1988-93 by the MathWorks Inc Modified by Oleg Alexandrov 2/16/03 if nargin < 6 color 0 0 0; end if nargin < 5 arrow_type 0; the default arrow it looks like this -> end if nargin < 4 sharpness pi/4; the arrow sharpness - default pi/4 end if nargin< 3 xl get gca 'xlim' ; yl get gca 'ylim' ; xd xl 2 -xl 1 ; yd yl 2 -yl 1 ; arrowsize xd + yd / 2; this sets the default arrow size end if nargin< 2 thickness 0 5; default thickness end xdif stop 1 - start 1 ; ydif stop 2 - start 2 ; if xdif 0 if ydif >0 theta pi/2; else theta -pi/2; end else theta atan ydif/xdif ; the angle has to point according to the slope end if xdif> 0 arrowsize -arrowsize; end if arrow_type 0 draw the arrow like two sticks originating from its vertex xx start 1 stop 1 stop 1 +0 02 arrowsize cos theta+sharpness NaN stop 1 stop 1 +0 02 arrowsize cos theta-sharpness ; yy start 2 stop 2 stop 2 +0 02 arrowsize sin theta+sharpness NaN stop 2 stop 2 +0 02 arrowsize sin theta-sharpness ; plot xx yy 'LineWidth' thickness 'color' color end if arrow_type 1 draw the arrow like an empty triangle xx stop 1 stop 1 +0 02 arrowsize cos theta+sharpness stop 1 +0 02 arrowsize cos theta-sharpness ; xx xx xx 1 xx 2 ; yy stop 2 stop 2 +0 02 arrowsize sin theta+sharpness stop 2 +0 02 arrowsize sin theta-sharpness ; yy yy yy 1 yy 2 ; plot xx yy 'LineWidth' thickness 'color' color plot the arrow stick plot start 1 stop 1 +0 02 arrowsize cos theta cos sharpness start 2 stop 2 + 0 02 arrowsize sin theta cos sharpness 'LineWidth' thickness 'color' color end if arrow_type 2 draw the arrow like a full triangle xx stop 1 stop 1 +0 02 arrowsize cos theta+sharpness stop 1 +0 02 arrowsize cos theta-sharpness stop 1 ; yy stop 2 stop 2 +0 02 arrowsize sin theta+sharpness stop 2 +0 02 arrowsize sin theta-sharpness stop 2 ; plot the arrow stick plot start 1 stop 1 +0 01 arrowsize cos theta start 2 stop 2 + 0 01 arrowsize sin theta 'LineWidth' thickness 'color' color H fill xx yy color ; fill with black set H 'EdgeColor' 'none' end if arrow_type 3 draw the arrow like a filled 'curvilinear' triangle curvature 0 5; change here to make the curved part more curved or less curved radius 0 02 arrowsize max curvature tan sharpness ; x1 stop 1 +0 02 arrowsize cos theta+sharpness ; y1 stop 2 +0 02 arrowsize sin theta+sharpness ; x2 stop 1 +0 02 arrowsize cos theta cos sharpness ; y2 stop 2 +0 02 arrowsize sin theta cos sharpness ; d1 sqrt x1-x2 2+ y1-y2 2 ; d2 sqrt radius 2-d1 2 ; d3 sqrt stop 1 -x2 2+ stop 2 -y2 2 ; center 1 stop 1 + d2+d3 cos theta ; center 2 stop 2 + d2+d3 sin theta ; alpha atan d1/d2 ; Alpha -alpha 0 05 alpha; xx center 1 -radius cos Alpha+theta ; yy center 2 -radius sin Alpha+theta ; xx xx stop 1 xx 1 ; yy yy stop 2 yy 1 ; plot the arrow stick plot start 1 center 1 -radius cos theta start 2 center 2 - radius sin theta 'LineWidth' thickness 'color' color ; H fill xx yy color ; fill with black set H 'EdgeColor' 'none' end </nowiki> </pre> 1 date/time username edit summary ---- 04 41 23 November 2005 en User Oleg Alexandrov <nowiki> fix bug </nowiki> ---- 04 34 23 November 2005 en User Oleg Alexandrov <nowiki> <span class autocomment ><a href /wiki/Image An_infinitely_differentiable_function_which_is_not_analytic_illustration png Source_code title Image An infinitely differentiable function which is not analytic illustration png > †’</a>Source code -</span> lang </nowiki> ---- 04 33 23 November 2005 en User Mathbot <nowiki> source_code </nowiki> ---- 04 32 23 November 2005 en User Oleg Alexandrov <nowiki> format </nowiki> ---- 04 29 23 November 2005 en User Oleg Alexandrov <nowiki></nowiki> Original upload log Legend cur this is the current file del delete this old version rev revert to this old version Click on date to download the file or see the image uploaded on that date del cur 04 43 23 November 2005 en User Oleg_Alexandrov Oleg Alexandrov en User_talk Oleg_Alexandrov Talk 500x146 6584 bytes differentiability functions Files by User Oleg Alexandrov from en wikipedia math | ||||