MAKE A MEME
View Large Image
| View Original: | Gause's experiment and fitted logistic curves.svg (489x208) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
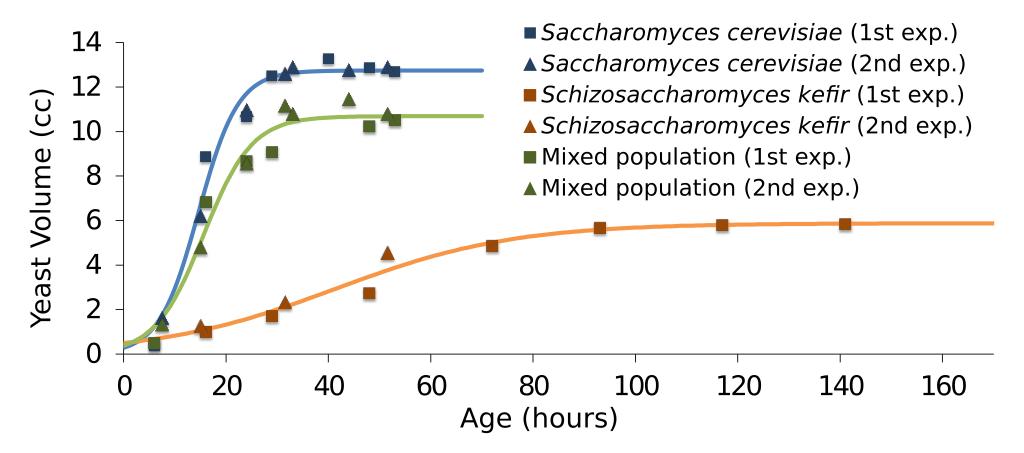
| Keywords: Gause's experiment and fitted logistic curves.svg ja ガウゼの実験結 <ref name Gause1932 > cite journal Gause G F 1932 Experimental Studies on the Struggle for Existence http //jeb biologists org/content/9/4/389 Journal of Experimental Biology The Company of Biologists Ltd 9 4 389-402 1477-9145 </ref>とレーベンバーグ・マーカート法でフィッティングさせたロジスティック曲線 <math>N \frac K 1+ K/N_0-1 e -rt </math> 下記のScilab（lsqrsolve）を使用して各パラメータ（r K N<sub>0</sub>）を求めた れらをもとにExcelでグラフ 成 InkscapeでSVG化 各曲線のパラメータは以下のとおり Saccharomyces cerevisiae N<sub>0</sub> 0 2831294 K 12 742142 r 0 2586369 Schizosaccharomyces kefir N<sub>0</sub> 0 4970908 K 5 8802335 r 0 0574421 Mixed population N<sub>0</sub> 0 3796836 K 10 690843 r 0 2116539 グラフ中の各 体群成長データはガウゼの論文のTable Iのデータを使用した en This figure shows Gause's experiment results<ref name Gause1932 /> and logistic curves fitted with Levenberg-Marquardt Method Logistic curve can be written as <math>N \frac K 1+ K/N_0-1 e -rt </math> Below Scilab lsqrsolve code was used to fit the parameters r K N<sub>0</sub> The fitted parameters of each curve are shown as follows Saccharomyces cerevisiae N<sub>0</sub> 0 2831294 K 12 742142 r 0 2586369 Schizosaccharomyces kefir N<sub>0</sub> 0 4970908 K 5 8802335 r 0 0574421 Mixed population N<sub>0</sub> 0 3796836 K 10 690843 r 0 2116539 The population growth data used in this graph are derived from Table I of Gause's paper <references /> 2016-02-13 own Yapparina other versions File Gause's experiment and fitted logistic curves single species svg Scilab source <source lang scilab > clear all; //data of Saccharomyces cerevisiae t1 6 7 5 15 16 24 24 29 31 5 33 40 44 48 51 5 53; y1 0 37 1 63 6 2 8 87 10 66 10 97 12 5 12 6 12 9 13 27 12 77 12 87 12 9 12 7; //th 1 N0 th 2 K th 3 r function e fun1 th m e y1-th 2 / 1+ th 2 /th 1 -1 exp -th 3 t1 ; endfunction parm v lsqrsolve 0 1;12;0 1 fun1 size t1 2 ; parm //data of Schizosaccharomyces kefir t2 15 16 29 31 5 48 51 5 72 93 117 141; y2 1 27 1 1 7 2 33 2 73 4 56 4 87 5 67 5 8 5 83; //th 1 N0 th 2 K th 3 r function e fun2 th m e y2-th 2 / 1+ th 2 /th 1 -1 exp -th 3 t2 ; endfunction parm v lsqrsolve 0 1;6;0 1 fun2 size t2 2 ; parm //data of Mixed population t3 6 7 5 15 16 24 24 29 31 5 33 44 48 51 5 53; y3 0 5 1 33 4 8 6 83 8 66 8 57 9 07 11 17 10 8 11 47 10 23 10 8 10 5; //th 1 N0 th 2 K th 3 r function e fun3 th m e y3-th 2 / 1+ th 2 /th 1 -1 exp -th 3 t3 ; endfunction parm v lsqrsolve 0 1;11;0 1 fun3 size t3 2 ; parm </source> cc-zero Logistic functions | ||||
