MAKE A MEME
View Large Image
| View Original: | Newton optimization vs grad descent.svg (650x749) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
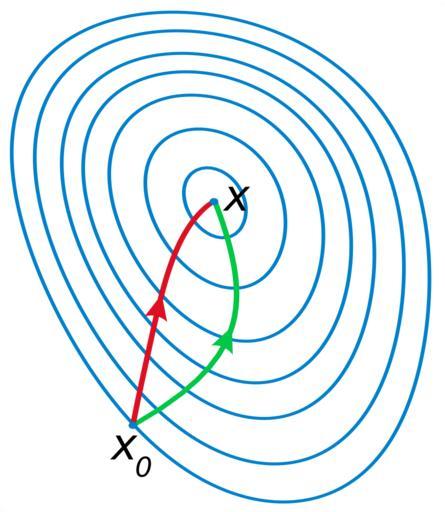
| Keywords: Newton optimization vs grad descent.svg A comparison of gradient descent green and Newton's method red for minimizing a function with small step sizes Newton's method uses curvature information to take a more direct route Porównanie metody najszybszego spadku linia zielona z metodą Newtona linia czerwona Na rysunku widać linie poszukiwań minimum dla zadanej funkcji celu Metoda Newtona używa informacji o krzywiźnie w celu zoptymalizowania ścieżki poszukiwań self-made with en Matlab Tweaked in en Inkscape 04 58 23 June 2007 UTC Oleg Alexandrov Source code <source lang matlab > Comparison of gradient descent and Newton's method for optimization function main the ploting window figure 1 ; clf; hold on; axis equal; axis off; colors red 0 867 0 06 0 14; blue 0 129 205/256; green 0 200 70/256; black 0 0 0; white 0 99 1 1 1; graphing settings lw 3; arrowsize 0 06; arrow_type 2; fs 13; the function whose contours will be plotted and its partials C 0 2 4 0 4 1 1 5; Tweak f by tweaking C f inline ' C 1 x-0 4 4+C 2 x 2+C 3 y+1 4+C 4 y 2+C 5 x y-1 ' 'x' 'y' 'C' ; fx inline ' 4 C 1 x-0 4 3+2 C 2 x+C 5 y ' 'x' 'y' 'C' ; fy inline ' 4 C 3 y+1 3+2 C 4 y+C 5 x ' 'x' 'y' 'C' ; fxx inline ' 12 C 1 x-0 4 2+2 C 2 ' 'x' 'y' 'C' ; fxy inline 'C 5 ' 'x' 'y' 'C' ; fyy inline ' 12 C 3 y+1 2+2 C 4 ' 'x' 'y' 'C' ; plot_contours f C blue white lw ; step size alpha 0 025; initial guess V0 -0 2182 -1 2585; x V0 1 ; y V0 2 ; z x; w y; run several iterations of gradient descent and Newton's method X x; Y y; Z z; W w; for i 0 200 grad descent u fx x y C ; v fy x y C ; x x-alpha u; y y-alpha v; X X x; Y Y y; newton's method u fx z w C ; v fy z w C ; mxx fxx z w C ; mxy fxy z w C ; myy fyy z w C ; M mxx mxy; mxy myy; V M\u; v; u V 1 ; v V 2 ; z z-alpha u; w w-alpha v; Z Z z; W W w; end plot X Y 'color' green 'linewidth' lw ; plot Z W 'color' red 'linewidth' lw ; plot text small 0 03; m length Z ; V Z m W m ; text V0 1 -2 small V0 2 -2 small 'x_0' 'fontsize' fs ; text V 1 +small V 2 +small 'x' 'fontsize' fs ; some small balls to hide some imperfections small_rad 0 015; ball V0 1 V0 2 small_rad blue ; ball V 1 V 2 small_rad blue ; save to eps ans svg saveas gcf 'Newton_optimization_vs_grad_descent eps' 'psc2' plot2svg 'Newton_optimization_vs_grad_descent svg' function plot_contours f C color color2 lw Calculate f on a grid Lx1 -2; Lx2 2; Ly1 -2; Ly2 2; N 60; h 1/N; XX Lx1 h Lx2; YY Ly1 h Ly2; X Y meshgrid XX YY ; Z f X Y C ; the contours h 0 3; l0 -1; l1 0 7; l0 h floor l0/h ; l1 h floor l1/h ; Levels -l0 1 5 h 0 0 h l1 0 78; Plot the contours with 'contour' in figure 2 and then with 'plot' in figure 1 This is to avoid a bug in plot2svg it can't save output of 'contour' figure 2 ; clf; hold on; axis equal; axis off; xmin 1000; ymin xmin; xmax -xmin; ymax -ymin; for i 1 length Levels figure 2 ; c stuff contour X Y Z Levels i Levels i ; m n size c ; if m > 1 n > 0 extract the contour from the contour matrix and plot in figure 1 l c 2 1 ; x c 1 2 l+1 ; y c 2 2 l+1 ; figure 1 ; plot x y 'color' color 'linewidth' 0 66 lw ; xmin min xmin min x ; xmax max xmax max x ; ymin min ymin min y ; ymax max ymax max y ; end end figure 1 ; some dummy text to expand the saving window a bit small 0 04; plot xmin-small ymin-small ' ' 'color' color2 ; plot xmax+small ymax+small ' ' 'color' color2 ; function arrow start stop thickness arrow_size sharpness arrow_type color Function arguments start stop start and end coordinates of arrow vectors of size 2 thickness thickness of arrow stick arrow_size the size of the two sides of the angle in this picture -> sharpness angle between the arrow stick and arrow side in radians arrow_type 1 for filled arrow otherwise the arrow will be just two segments color arrow color a vector of length three with values in 0 1 convert to complex numbers i sqrt -1 ; start start 1 +i start 2 ; stop stop 1 +i stop 2 ; rotate_angle exp i sharpness ; points making up the arrow tip besides the stop point point1 stop - arrow_size rotate_angle stop-start /abs stop-start ; point2 stop - arrow_size/rotate_angle stop-start /abs stop-start ; if arrow_type 1 filled arrow plot the stick but not till the end looks bad t 0 5 arrow_size cos sharpness /abs stop-start ; stop1 t start+ 1-t stop; plot real start stop1 imag start stop1 'LineWidth' thickness 'Color' color ; fill the arrow H fill real stop point1 point2 imag stop point1 point2 color ; set H 'EdgeColor' 'none' else two-segment arrow plot real start stop imag start stop 'LineWidth' thickness 'Color' color ; plot real stop point1 imag stop point1 'LineWidth' thickness 'Color' color ; plot real stop point2 imag stop point2 'LineWidth' thickness 'Color' color ; end function ball x y r color Theta 0 0 1 2 pi; X r cos Theta +x; Y r sin Theta +y; H fill X Y color ; set H 'EdgeColor' 'none' ; </source> Optimization Newton Method Files by User Oleg Alexandrov from en wikipedia Images with Matlab source code | ||||