MAKE A MEME
View Large Image
| View Original: | Transformation (after).png (996x798) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
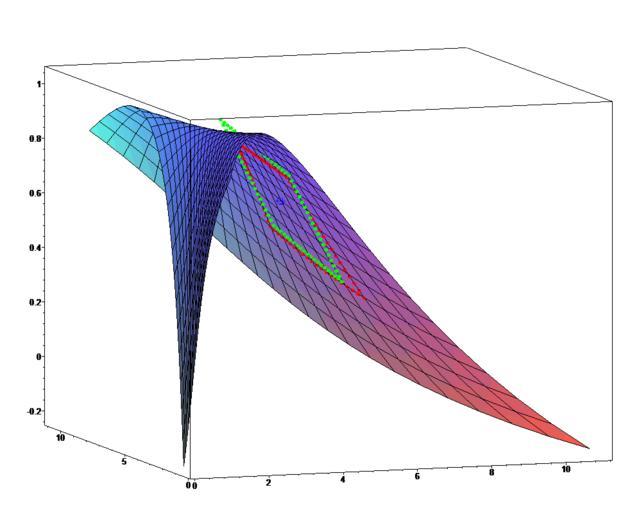
| Keywords: Transformation (after).png This image is part of a collection of 2 plots of mathemical functions other image Transformation_ before png They show a strongly non-linear w transformation mathematics being applied to a simple function a plane through the origin The plane is transformed into a a curved surface The transformaton is the following <math> u v w \mapsto e u+v e u-v \cos \left w \right </math> legend ;blue dot reference point ;red dots reference square ;green dots the reference square transformed by a w linear approximation of the non-liear transformation created with Maple 10 using the following code <code> <pre> > restart with VectorCalculus with plots with plottools z x y ->sin 1/2 x 2-1/4 y 2+3 cos 2 x+1-exp y > z x y ->x+y/2 > t1 u v w -> exp u+v exp u-v cos w ; > ti t1 x y z ; > bt x y z x y ; > bl t1 bt ; > pc 1/2 1/2; > p0 pc1 pc2 z pc1 pc2 ; > myunit 0 3; > circum map p->p1 p2 z p1 p2 pc+myunit i/5 myunit i -10 10 pc+-myunit i/10 myunit i -10 10 pc+i/10 myunit myunit i -10 10 pc+i/10 myunit -myunit i -10 10 > i0 evalf t1 p0 ; > display plot3d x y z x y x -1 2 1 2 y -1 2 1 2 axes normal point p0 color blue symbol circle symbolsize 10 'point circumi color red symbol circle symbolsize 2 ' 'i' 1 nops circum ; > display plot3d bl x -1 2 1 2 y -1 2 1 2 axes normal point i0 color blue symbol circle symbolsize 10 'point t1 circumi color red symbol circle symbolsize 2 ' 'i' 1 nops circum ; > J Jacobian ti x y z ; > lindiff Matrix eval J x p01 y p02 z p03 ; > tl u v w ->convert lindiff Vector u v w list ; > evalf tl 0 0 0 ; > evalf t1 p0 ; > linapp map c->evalf i0+tl c-p0 circum > display plot3d bl x -1 2 1 2 y -1 2 1 2 axes normal point i0 color blue symbol circle symbolsize 10 'point t1 circumi color red symbol circle symbolsize 2 ' 'i' 3 nops circum 'point linappi color green symbol circle symbolsize 2 ' 'i' 4 nops circum ; > display 'point linappi-t1 circumi color green symbol circle symbolsize 2 ' 'i' 1 nops circum ; </pre> </code> Surface plots Maple diagrams Transformations geometry | ||||